What is Cryptography?
Cryptography is the study of secure communications techniques that allow only the sender and intended recipient of a message to view its contents. Specifically, these techniques are used to protect information that is obtained from mathematical concepts and a set of rule-based calculations or algorithms to convert messages, making them difficult to decode.
Originating back to Ancient Egypt, cryptography was believed to be used by Ancient Egyptians in complex hieroglyphics. Roman Emperor Julius Caesar has been credited with using one of the first modern ciphers.
Cryptography can be split into two eras--the classical era and the modern era. The turning point occurred in 1977 with the RSA algorithm and the Diffie-Hellman key exchange algorithm. More on that later.
Types of Cryptography
Traditionally, there are three types of cryptography: symmetric key, hash functions, and asymmetric key.
Symmetric Key
This is an encryption system where the sender and receiver of a message uses a single common key to encrypt and decrypt messages. While this method is faster and simpler than the other two methods, it is up to the sender and receiver to exchange the key in a secure manner.
The most popular example of this is Data Encryption System (DES). Let’s try the following example:
You have a message, “M”, you want to sent to your friend. You encrypt the message with a Key and get a cipher text, “C”.
Your friend gets the cipher text, C, to which she then decrypts the cipher text using the same Key to retrieve M.
There are two types of symmetric cryptography: stream ciphers and block ciphers.
Stream Ciphers
A stream cipher uses a fixed key that replaces the message with a pseudorandom string of characters. It encrypts each letter, one at a time.
For more information on steam ciphers, please click here.
Block Ciphers
These are a form of symmetric cryptography which uses a key of a fixed length to encrypt a block of fixed length.
For more information on block ciphers, please click here.
Hash Functions
In a Hash Function system, there is no key. Instead, a hash value with a fixed length is calculated based on the text, making it impossible for the contents of plain text to be recovered. Many operating systems use hash functions to encrypt passwords.
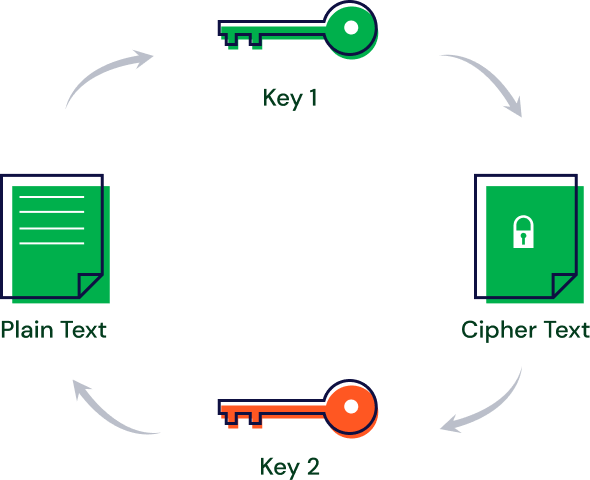
Asymmetric Key (Public Key)
Under this cryptography system, a pair of keys is used to encrypt and decrypt information. The public key is used for encryption and a private key for decryption. Even if the public key is known by everyone, the intended receiver can only decode it because they alone know the private key.
Cryptocurrency
How does cryptography help ensure that cryptocurrency transactions are secure?
Digital Signatures
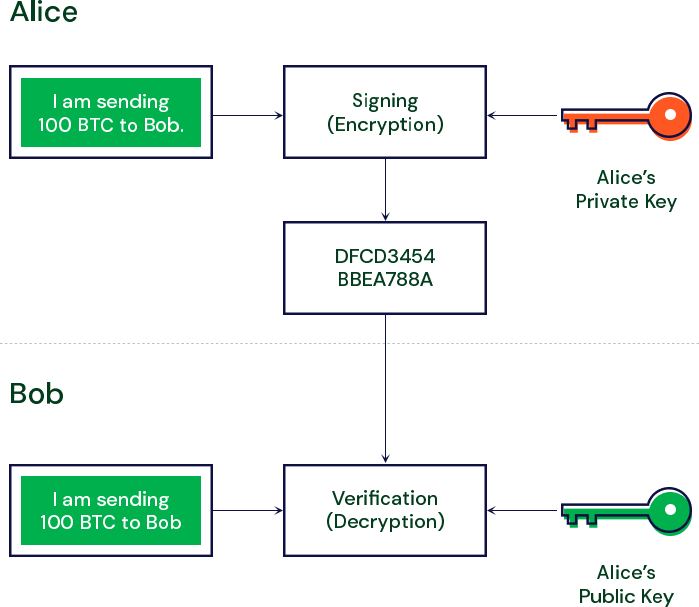
In cryptocurrency, one of the most important cryptographic tools is the use of digital signatures. Digital signatures are cryptographic values that are calculated from the data and a secret key known only by the signer. Each person has a public/private key pair.
Diffie-Hellman Key Exchange

Let’s assume Alice and Bob want to rob a bank, how are they going to accomplish this without explicitly sharing information?
Enter the Diffie-Hellman Key Exchange. This allows for two parties who have never met, to securely establish a key to help secure their communications and transfer information back and forth.
This has become one of the most important developments in public-key cryptography today, dating back to the 1970s. The Diffie-Hellman key exchange was the first widely used method of safely developing and exchanging keys over an insecure channel.
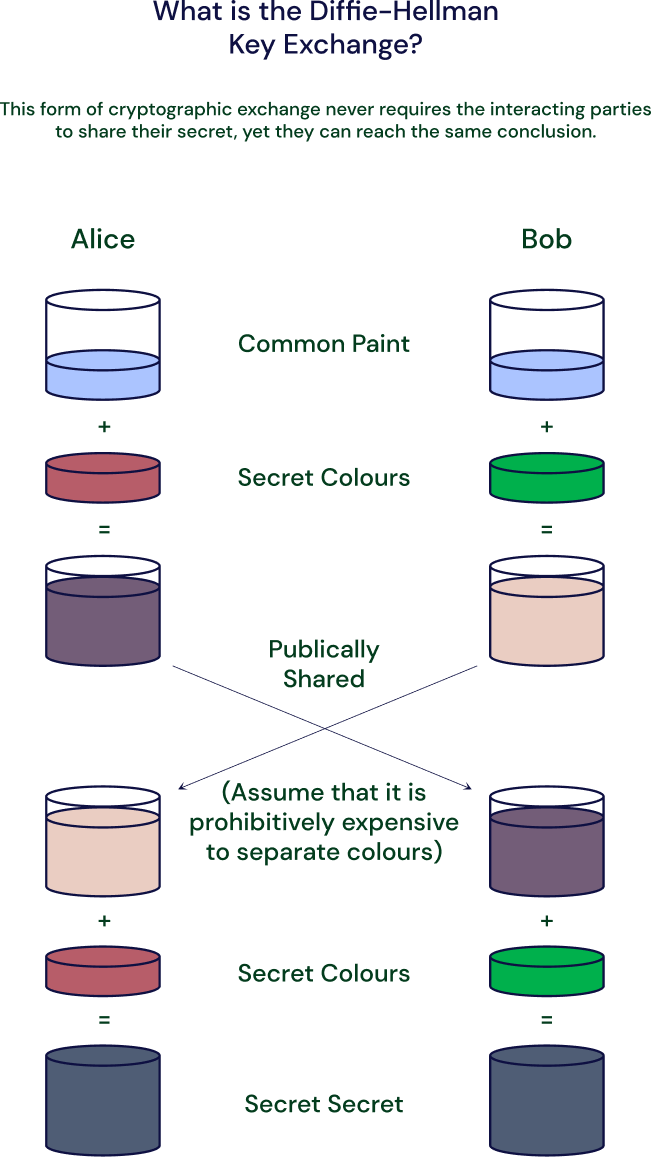
The easiest way to explain the key exchange is by using the secret paint example--let’s say Alice and Bob each agree on a random color of the paint.
Now they need to send each other a message and decide (together) that yellow is the common color. But they cannot tell the other party their choice.
Alice chooses red, while Bob chooses a slightly-greenish blue.
Digital Signatures
The next step requires both Alice and Bob to mix their secret color (red for Alice, greenish-blue for Bob) with the yellow that they mutually agreed upon. As a result, Alice ends up with an orangish mix, while Bob’s result is a deeper blue.
Once they have finished mixing, they send their final result to the other, with Alice receiving the deeper blue and Bob receiving the orange-colored paint.
Once they have received the final result, they add their secret color to it, with Alice adding her secret red paint to her deeper blue, while Bob adds his secret greenish-blue to the orange mix.
The outcome? They both come out with the same color, which in this case, is a nasty looking brown. It is a shared color, or common secret, as it’s referred to.
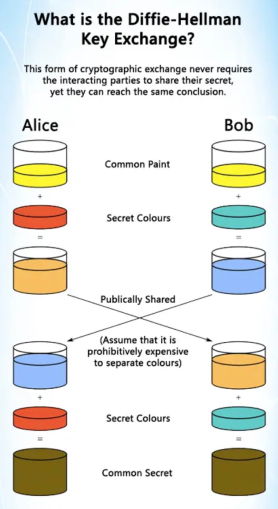
The takeaway here, in applying the Diffie-Hellman key exchange analogy, is that both parties end up with the same result, without ever needing to send that common secret across the insecure communication channel. For more information, please click here.
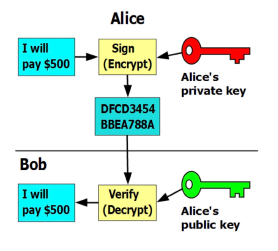
Signing a Transaction
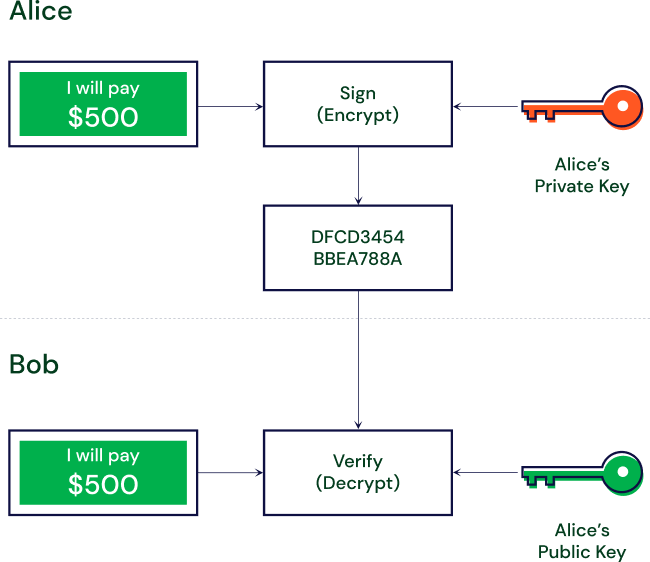
Let’s say Alice wants to send 500 BTC to Bob. She will need to:
- Create a transaction and sign off on it with her private key
- She will then send that transaction to Bob’s public address
- Upon receipt, Bob is then able to decrypt the message using Alice’s public key to verify that it was Alice who sent him the 500 BTC. Once this is done, the transaction is complete.
Elliptical Curve Cryptography
After RSA and Diffie-Hellman were introduced, researchers explored other mathematics-based crypto solutions, looking for other algorithms. In 1985, elliptic curves were proposed.
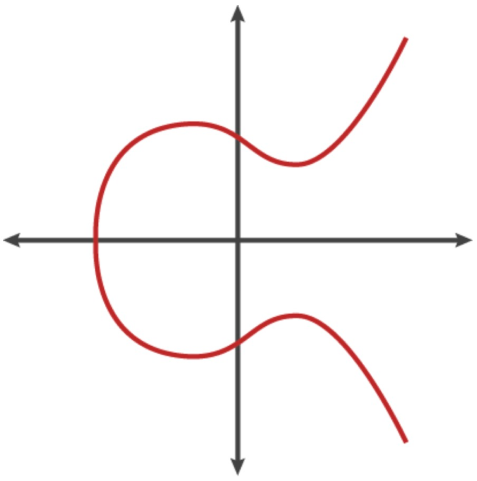
An elliptic curve is the set of points that satisfy a specific mathematical equation. That equation looks like: y2 = x3 + ax + b
The graph depicting this equation looks like:
y2 = x3 + ax + b
For more information on how elliptic curves function, please click here.